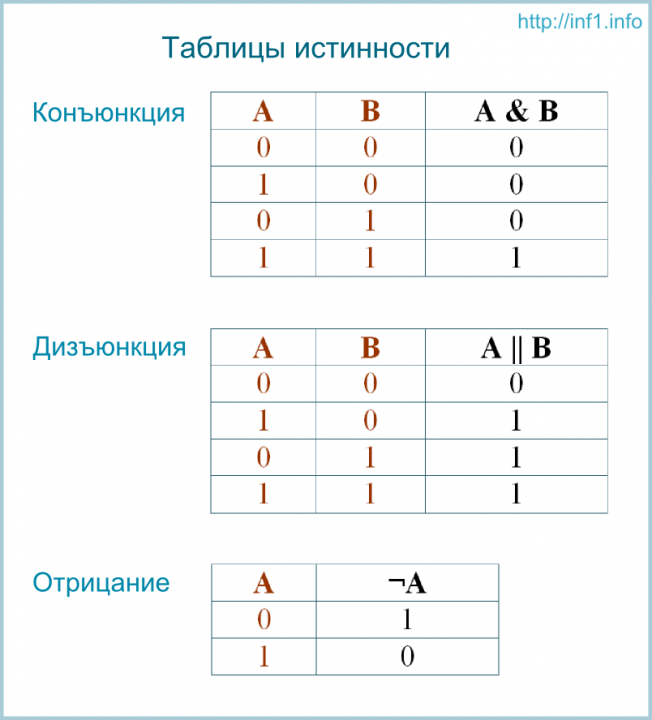
Алгебра логики – это раздел математики, изучающий основные принципы и законы логических операций. В основе этой алгебры лежит идея описания и преобразования логических выражений с использованием символов и операций, аналогичных арифметическим операциям. Закон алгебры логики представляет собой основные правила и свойства, которые позволяют сокращать и упрощать выражения, а также строить функциональные схемы и таблицы истинности для логических операций.
В алгебре логики существуют несколько основных законов, которые позволяют упрощать выражения и проводить логические преобразования. Одним из таких законов является закон дистрибутивности. Согласно этому закону, операция «или» и операция «и» можно распределить относительно друг друга. Другими словами, выражение a ∨ (b ∧ c) эквивалентно (a ∨ b) ∧ (a ∨ c), а выражение a ∧ (b ∨ c) эквивалентно (a ∧ b) ∨ (a ∧ c). Закон дистрибутивности позволяет упростить сложные логические выражения и сделать их более понятными и компактными.
Еще одним важным законом алгебры логики является закон де Моргана. Согласно этому закону, отрицание конъюнкции или дизъюнкции равносильно конъюнкции или дизъюнкции отрицаний соответствующих выражений. Другими словами, отрицание выражения (a ∧ b) эквивалентно ¬a ∨ ¬b, а отрицание выражения (a ∨ b) эквивалентно ¬a ∧ ¬b. Закон де Моргана также позволяет упрощать логические выражения, особенно когда они содержат отрицания.
Основные принципы закона алгебры логики
Основные принципы закона алгебры логики включают:
Принцип тождества: существует нейтральный элемент для каждой операции. Например, в случае операции «и» нейтральным элементом является истина, а в случае операции «или» нейтральным элементом является ложь.
Принцип противоположности: для каждого элемента существует противоположный элемент. Например, противоположным элементом для истины является ложь, а для лжи – истина.
Принцип дистрибутивности: операции можно распределить относительно друг друга. Например, дистрибутивность операции «или» относительно операции «и» означает, что a или (b и c) эквивалентно (a или b) и (a или c).
Принцип ассоциативности: порядок выполнения операций не влияет на результат. Например, (a или b) или c эквивалентно a или (b или c).
Принцип коммутативности: порядок элементов не влияет на результат. Например, a и b эквивалентно b и a.
Эти основные принципы закона алгебры логики позволяют упростить и систематизировать логические рассуждения, а также основываться на строгих математических принципах при работе с логическими выражениями.
Коммутативный закон
Другими словами, коммутативный закон говорит о том, что результат операции не зависит от того, в каком порядке операнды расположены.
Например, в алгебре логики коммутативный закон применяется для операций «И» (логическое умножение) и «ИЛИ» (логическое сложение).
Пример:
Для операции «И»:
1 ⋆ 0 = 0 ⋆ 1 = 0
1 ⋆ 1 = 1 ⋆ 1 = 1
Для операции «ИЛИ»:
1 ⋆ 0 = 0 ⋆ 1 = 1
0 ⋆ 0 = 0 ⋆ 0 = 0
Коммутативный закон позволяет упростить выражения и сократить количество операций в алгебре логики. Он является одним из основных принципов, которые позволяют строить логические цепочки и схемы.
Ассоциативный закон
Согласно ассоциативному закону, при выполнении операции над трёмя или более элементами, порядок их группировки не влияет на результат.
Для операции сложения обозначается символом «+». Например, для выражения «a + (b + c)», ассоциативный закон гласит: «a + (b + c) = (a + b) + c».
Ассоциативный закон применим и для операции умножения, обозначаемой символом «⋅». Например, для выражения «a ⋅ (b ⋅ c)», ассоциативный закон гласит: «a ⋅ (b ⋅ c) = (a ⋅ b) ⋅ c».
Ассоциативный закон позволяет изменять порядок операций в выражении без изменения его смысла и результата. Это удобно при решении сложных логических задач и способствует более читаемому и понятному представлению выражений.
Важно отметить, что ассоциативный закон не действует для всех операций в алгебре логики. Например, для операции вычитания и операции деления ассоциативный закон не выполняется.
Дистрибутивный закон
Дистрибутивный закон для конъюнкции (логического умножения):
Если дано выражение вида (A ∧ B) ∨ C, то его можно преобразовать с помощью дистрибутивного закона следующим образом:
(A ∧ B) ∨ C = (A ∨ C) ∧ (B ∨ C).
Дистрибутивный закон для дизъюнкции (логического сложения):
Если дано выражение вида (A ∨ B) ∧ C, то его можно преобразовать с помощью дистрибутивного закона следующим образом:
(A ∨ B) ∧ C = (A ∧ C) ∨ (B ∧ C).
Дистрибутивный закон имеет большое значение при работе с логическими операциями, так как он позволяет упростить и анализировать сложные логические выражения. Этот закон часто используется при доказательстве тождеств и при решении логических задач.
Примеры применения закона алгебры логики
Пример 1: Распределительный закон
Распределительный закон гласит, что логическая операция «или» (||) может быть распределена внутри логической операции «и» (&&), и наоборот. Например:
| Выражение | Упрощенное выражение |
|---|---|
| (A && B) || (A && C) | A && (B || C) |
| (A || B) && (A || C) | A || (B && C) |
Пример 2: Двойное отрицание
Закон двойного отрицания утверждает, что двойное отрицание любого выражения равно самому выражению. Например:
| Выражение | Упрощенное выражение |
|---|---|
| !!A | A |
| !!(A && B) | A && B |
Пример 3: Закон исключения третьего
Закон исключения третьего утверждает, что любое выражение или его отрицание истинно. Например:
| Выражение | Упрощенное выражение |
|---|---|
| A || !A | true |
| (A && !B) || !(A && !B) | true |
Пример 4: Закон импликации
Закон импликации утверждает, что логическое выражение «если A, то B» может быть выражено с помощью логической операции «или» (||) и отрицания. Например:
| Выражение | Упрощенное выражение |
|---|---|
| A => B | !A || B |
| (A && B) => C | !(A && B) || C |
Это лишь некоторые из множества законов алгебры логики, которые могут быть применены для упрощения и анализа логических выражений. Знание этих законов позволяет производить логические операции и упрощать сложные выражения в более простые формы.
Пример 1: Упрощение логических выражений
Рассмотрим пример:
Исходное выражение: A ∩ (B ∪ C)
Для начала разберемся с операцией дизъюнкции (B ∪ C). Она означает «или» и будет истинной, если хотя бы один из операндов истинный. Поэтому, если B истинно или C истинно, то результатом дизъюнкции будет истина.
Заменим операцию дизъюнкции выражением, которое она представляет:
A ∩ (B ∪ C) = A ∩ (B + C)
Примечание: символ + в данном случае также используется как обозначение операции дизъюнкции.
Теперь обратимся к операции конъюнкции A ∩ (B + C). Она означает «и» и будет истинной, только если все операнды истинны. Поэтому, результатом конъюнкции будет истина только в случае, когда и A, и (B + C) истинны.
Однако, заметим, что если A истино, то результат всего выражения уже будет истиной, независимо от значения (B + C). Таким образом, можно записать выражение более простым образом:
A ∩ (B + C) = A
Итак, мы упростили изначальное выражение A ∩ (B ∪ C) до более компактного и понятного выражения A. Такое упрощение может быть полезным при анализе больших и сложных логических выражений, поскольку сокращает количество операций и переменных, с которыми нужно работать.
Пример 2: Построение таблиц истинности
Для понимания принципов и законов алгебры логики важно уметь строить таблицы истинности. Таблица истинности позволяет проанализировать все возможные комбинации значений для заданных логических выражений и определить, при каких условиях выражение будет истинным или ложным.
Рассмотрим пример таблицы истинности для простого логического выражения: (p ∧ q) ∨ r.
Для выражения (p ∧ q) ∨ r существуют три переменные: p, q и r, каждая из которых может принимать два значения — истина (1) или ложь (0). Таким образом, для данного выражения существует 2^3 = 8 различных комбинаций значений переменных.
Таблица истинности для выражения (p ∧ q) ∨ r выглядит следующим образом:
| p | q | r | (p ∧ q) ∨ r |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
В данной таблице истинности мы вычисляем значение выражения (p ∧ q) ∨ r для каждой комбинации значений переменных и записываем результат.
Таким образом, таблица истинности позволяет наглядно представить, при каких значениях переменных логическое выражение будет равно истине (1) или лжи (0).
Вопрос-ответ:
Зачем нужен закон алгебры логики?
Закон алгебры логики позволяет систематизировать и формализовать процесс логического рассуждения. Это помогает в решении задач и принятии верных логических выводов.
Какие основные принципы лежат в основе алгебры логики?
Основными принципами алгебры логики являются идемпотентность, коммутативность, дистрибутивность, ассоциативность, нейтральность, а также отрицание, импликация и эквивалентность.
Можете привести примеры использования алгебры логики в реальной жизни?
Алгебра логики может быть использована в различных областях, таких как информационные технологии, криптография, математика, философия, электроника и другие. Например, в информатике алгебра логики используется для проектирования логических схем и создания программного обеспечения, а в криптографии — для разработки безопасных алгоритмов шифрования.
Какие варианты имеет отрицание в алгебре логики?
В алгебре логики существуют два варианта отрицания: обычное отрицание (NOT) и отрицание по модулю два (NAND). Обычное отрицание инвертирует значение логической переменной, а отрицание по модулю два возвращает значение, противоположное результату логической операции.
Можно ли использовать алгебру логики для решения повседневных задач?
Да, алгебра логики может быть применена для решения повседневных задач, например, при планировании расписания, принятии решений или построении логической модели процесса. Она помогает систематизировать информацию и анализировать возможные варианты.
Что такое закон алгебры логики?
Закон алгебры логики — это основной принцип, согласно которому выполняются операции с логическими значениями и выражениями. Он определяет правила, которым должны следовать операции с булевыми значениями, такими как «И» (конъюнкция), «ИЛИ» (дизъюнкция), «НЕ» (отрицание) и т.д. Эти законы позволяют упростить выражения и проверять их истинность.