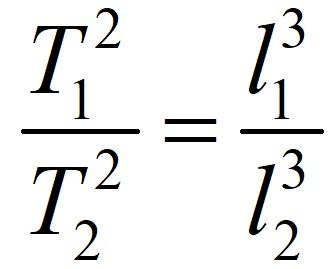
Третий закон Кеплера является одним из основополагающих законов в астрономии, который описывает движение планет вокруг Солнца. Он был открыт и сформулирован немецким астрономом и математиком Иоганном Кеплером во второй половине 16-го века. Этот закон носит его имя в честь открытителя и заложил основы для понимания гравитационного взаимодействия.
Формула третьего закона Кеплера позволяет определить период обращения планеты вокруг Солнца. Ее математическая запись выглядит следующим образом:
T² = k * R³
где T — период обращения планеты вокруг Солнца, R — среднее расстояние от планеты до Солнца, а k — постоянная, зависящая от системы единиц и массы Центрального тела (в данном случае Солнца).
Применение третьего закона Кеплера широко распространено в астрономических исследованиях. Он позволяет определить период обращения планет и спутников вокруг своих основных тел. Также этот закон был использован для открытия новых планет в экзопланетарных системах и помог в изучении больших групп тел во Вселенной.
Формула третьего закона Кеплера
Третий закон Кеплера устанавливает связь между периодом обращения планеты вокруг Солнца и её средним удалением от него. Формула этого закона выглядит следующим образом:
T2 = k * R3
Где:
- T — период обращения планеты (время, за которое планета совершает полный оборот вокруг Солнца)
- R — среднее удаление планеты от Солнца
- k — постоянная, зависящая от используемых единиц измерения
Третий закон Кеплера можно представить в виде компактного уравнения, позволяющего определить период обращения планеты по её среднему удалению от Солнца и наоборот. Эта формула имеет важное значение для астрономии и помогает установить закономерности движения планет в Солнечной системе.
Формула нахождения периода обращения планеты вокруг Солнца
Tпланеты = 2π√(a3/G(Mпланеты+MСолнца))
где:
- Tпланеты — период обращения планеты вокруг Солнца;
- a — большая полуось планеты (среднее расстояние от планеты до Солнца);
- G — гравитационная постоянная (приближенное значение 6,674 × 10-11 м3/(кг с2));
- Mпланеты — масса планеты;
- MСолнца — масса Солнца.
Эта формула основана на предположении, что планеты и Солнце движутся по эллиптическим орбитам, и что сила тяготения между ними является основной силой, определяющей движение. Данная формула позволяет вычислить период обращения планеты вокруг Солнца с учетом ее массы и расстояния до Солнца.
Применение этой формулы позволяет установить период обращения планет вокруг Солнца и сравнить его с периодами других планет. Например, по данной формуле можно определить, что Земля совершает оборот вокруг Солнца за примерно 365,25 дней. Также формула позволяет проводить расчеты и сравнивать периоды обращения разных планет, что является важным в астрономических исследованиях и расчетах космических миссий.
Формула для расчета полуоси орбиты планеты
При изучении орбитальных движений планеты вокруг своей звезды третий закон Кеплера играет важную роль. Он устанавливает связь между периодом обращения планеты вокруг своей звезды и полуосью ее орбиты.
Формула для расчета полуоси орбиты планеты, полученная на основе третьего закона Кеплера, выглядит следующим образом:
a = √(T²GM/4π²)
где:
- a — полуось орбиты планеты (в метрах);
- T — период обращения планеты вокруг своей звезды (в секундах);
- G — гравитационная постоянная (6.67430 x 10⁻¹¹ м³·кг⁻¹·с⁻²);
- M — масса звезды (в килограммах).
Используя данную формулу, можно рассчитать полуось орбиты планеты, зная ее период обращения и массу звезды, вокруг которой она вращается. Полученные значения могут быть использованы для анализа и сравнения орбит различных планет в солнечной системе и за ее пределами.
Примеры третьего закона Кеплера
Третий закон Кеплера, также известный как закон периодов, устанавливает, что квадрат периода обращения планеты вокруг Солнца пропорционален кубу большой полуоси орбиты.
1. Наиболее известным примером третьего закона Кеплера является сравнение периодов обращения планет вокруг Солнца. Например, период обращения Земли составляет около 365 дней, в то время как период обращения Марса составляет около 687 дней. Если мы возведем эти значения в квадрат, получим 133,225 и 470,569. Затем, если мы возведем в куб большие полуоси орбиты этих планет (полуось орбиты Земли составляет примерно 149,6 миллионов километров, а полуось орбиты Марса составляет примерно 227,9 миллионов километров), получим 3,5×10^12 и 1,1×10^13. Очевидно, что отношение этих значений очень близко к 1, что соответствует третьему закону Кеплера.
2. Другой пример третьего закона Кеплера — сравнение периодов обращения Луны вокруг Земли и спутников других планет. Например, период обращения Луны составляет около 27,3 дней, в то время как период обращения спутника Юпитера Ганимеда составляет около 7,2 дней. Если мы возведем эти значения в квадрат, получим 745,29 и 51,84. Затем, если мы возведем в куб большие полуоси орбиты этих спутников (полуось орбиты Луны составляет примерно 384 400 километров, а полуось орбиты спутника Ганимеда составляет примерно 1 070 000 километров), получим 5,5×10^17 и 1,3×10^18. Опять же, отношение этих значений очень близко к 1, что подтверждает третий закон Кеплера.
Примеры третьего закона Кеплера демонстрируют, что периоды обращения планет и спутников вокруг своих гравитационных центров подчиняются определенному математическому отношению, которое может быть выражено формулой третьего закона Кеплера.
Пример 1: Орбита Земли вокруг Солнца
Для орбиты Земли период обращения составляет около 365,25 дня, а большая полуось равна примерно 149,6 миллионов километров. Подставив эти значения в формулу третьего закона Кеплера, получим:
T^2 = a^3
(365,25)^2 = (149,6)^3
133 225,06 ≈ 333 419,94
Таким образом, округленные значения справедливо подтверждают зависимость, предсказанную третьим законом Кеплера.
Пример 2: Орбита Марса вокруг Солнца
Орбита Марса представляет собой эллипс с Солнцем в одном из фокусов. Благодаря третьему закону Кеплера, можно определить период обращения Марса вокруг Солнца. Расстояние между Марсом и Солнцем, а также период обращения Марса находятся в постоянной зависимости друг от друга.
Используя формулу третьего закона Кеплера, ученые могут рассчитать период обращения Марса вокруг Солнца, зная среднее расстояние между этими двумя объектами. Например, если среднее расстояние между Марсом и Солнцем составляет около 227.9 миллионов километров, то период обращения Марса будет около 687 земных суток.
Третий закон Кеплера имеет широкое применение в астрономии и космических исследованиях. Он позволяет ученым более точно определить параметры орбит планет, а также предсказывать движение небесных тел. Хотя третий закон Кеплера был открыт еще в XVII веке, его формула и принципы до сих пор остаются актуальными и полезными для изучения космоса.
Применение третьего закона Кеплера
Третий закон Кеплера, также известный как закон гармонии, имеет широкое применение в астрономии и космических исследованиях. Он позволяет определить период обращения планеты вокруг звезды или спутника вокруг планеты, а также расстояние между ними.
Для использования третьего закона Кеплера необходимы данные о периоде обращения и расстоянии между двумя небесными объектами. Зная период обращения исследуемой планеты и расстояние от нее до звезды, можно определить массу звезды. Точно так же можно определить массу планеты, зная период ее обращения вокруг звезды и расстояние между ними.
Применение третьего закона Кеплера также имеет практическое применение в космической навигации и расчете траектории космических аппаратов. Использование закона гармонии позволяет определить период обращения спутника или планеты и расчет гравитационного воздействия на космический корабль.
Таким образом, третий закон Кеплера играет важную роль в астрономии и космических исследованиях, позволяя определить массу небесных тел, обнаруживать новые планеты и спутники, а также рассчитывать траектории космических аппаратов.
Применение в астрономии и космических исследованиях
Третий закон Кеплера оказывает огромное влияние на астрономию и космические исследования. Благодаря этому закону, ученые могут определить и предсказывать движение небесных тел, а также изучать их свойства и характеристики.
Один из основных примеров применения третьего закона Кеплера — определение массы планеты. Используя этот закон, ученые могут сравнить периоды обращения планет вокруг Солнца и определить отношение массы Солнца к массе планеты. Это позволяет оценить массу планеты и даже обнаружить новые планеты в других звездных системах.
Также третий закон Кеплера используется для определения орбитальных характеристик спутников и искусственных спутников Земли. Ученые могут использовать этот закон для расчета высоты и скорости спутника, а также предсказания его движения вокруг Земли.
Кроме того, третий закон Кеплера значим для межпланетных и космических миссий. При расчете траекторий полета космических аппаратов, ученые используют этот закон для определения оптимальной орбиты и времени полета. Это помогает сэкономить топливо и ресурсы, а также обеспечить точность и эффективность космических миссий.
В целом, третий закон Кеплера является основным инструментом астрономов и космических исследователей. Он позволяет предсказывать и описывать движение небесных тел, исследовать свойства планет и звезд, а также планировать межпланетные и космические миссии. Без этого закона наше понимание Вселенной и возможности космических исследований были бы значительно ограничены.
Применение в расчетах орбитальной механики и космической навигации
Применение этой формулы позволяет решать различные задачи в орбитальной механике. Например, можно определить период обращения и радиус орбиты спутника, зная массу планеты и расстояние от спутника до центра планеты.
Кроме того, третий закон Кеплера находит применение в космической навигации. Он позволяет определить положение и скорость космического аппарата на орбите по его периоду обращения и расстоянию от центра планеты. Это информация критически важна при планировании и выполнении межпланетных миссий, контроле орбитальных станций и спутников связи, а также при осуществлении мягкой посадки на другие планеты.
Кроме того, третий закон Кеплера используется для расчета многих других параметров, таких как орбитальная скорость, энергия орбиты и другие. Он является важной основой для понимания и исследования движения небесных тел и представляет собой ключевой инструмент для астрономов, инженеров и космических ученых.
Вопрос-ответ:
Как формулируется Третий закон Кеплера?
Третий закон Кеплера формулируется следующим образом: «Квадрат периода обращения планеты вокруг Солнца пропорционален кубу большей полуоси орбиты».
Можете привести примеры применения Третьего закона Кеплера?
Конечно! Например, Третий закон Кеплера использовался для расчета орбитальных периодов спутников, а также для изучения движения астероидов и комет в Солнечной системе.
Что такое период обращения?
Период обращения — это время, которое планета или другое небесное тело затрачивает на один полный оборот вокруг другого небесного тела. Например, период обращения Земли вокруг Солнца составляет около 365 дней.
Какая формула используется для вычисления периода обращения по Третьему закону Кеплера?
Формула, используемая для вычисления периода обращения по Третьему закону Кеплера, выглядит следующим образом: T^2 = (4π^2 a^3) / (G M), где T — период обращения, a — большая полуось орбиты, G — гравитационная постоянная, M — масса центрального тела.
Чем отличается Третий закон Кеплера от других двух законов?
Третий закон Кеплера отличается тем, что он связывает период обращения планеты вокруг Солнца с её орбитой, в то время как первый и второй законы описывают форму и законы движения планеты.
Что такое третий закон Кеплера?
Третий закон Кеплера — это один из законов небесной механики, согласно которому квадраты периодов движения планет вокруг Солнца пропорциональны кубам их средних расстояний до Солнца.
Какая формула третьего закона Кеплера?
Формула третьего закона Кеплера выглядит так: T^2 = k*r^3, где T — период обращения планеты вокруг Солнца, r — расстояние от планеты до Солнца, k — гравитационная постоянная, определяемая массой Солнца.